2.0 Sljedeći modul Tekućine, otopine i koloidni sustavi
1.4

Usustavljivanje gradiva o energiji i kemijskim promjenama

Moći ću:
  • izračunati reakcijsku entalpiju na temelju promjene entalpije tijekom kemijske reakcije i množine utrošenog reaktanta/nastalog produkta
  • prikazati entalpijskim dijagramom odnose entalpija reaktanata i produkata te smjer reakcijske promjene
  • povezati potencijalnu i kinetičku energiju čestica s unutarnjom energijom sustava.

Povlačenjem elemenata uskladi odgovarajuće parove.

Spojite parove premještajući pojmove po stupcima.

Oznakama za standardne entalpije pridružite pojam.

entalpija isparavanja
\Delta_\textrm{r}H^\circ

entalpija taljenja
\Delta_\textrm{s}^\textrm{l}H^\circ

entalpija kondenzacije
\Delta_\textrm{l}^\textrm{s}H^\circ

entalpija kristalizacije
\Delta_\textrm{c}H^\circ

entalpija sublimacije
\Delta_\textrm{l}^\textrm{g}H^\circ

reakcijska entalpija
\Delta_\textrm{s}^\textrm{g}H^\circ

entalpija nastajanja elementarnih tvari
\Delta_\textrm{g}^\textrm{l}H^\circ

entalpija izgaranja
\Delta_\textrm{f}H^\circ
Netočno
Točno
{{correctPercent}}%

Želite li pokušati ponovo?

Povlačenjem elemenata uskladi odgovarajuće parove.

Spojite parove premještajući pojmove po stupcima.

Fizikalnim veličinama pridružite odgovarajuću mjernu jedinicu.

\Delta t
\pu{^\circ C}
\Delta_{\textrm{b}}H^\circ
\pu{kJ mol-1}

c
\pu{J mol-1K-1}
\Delta U
\pu{J K-1}
C_{\textrm{m}}

J

C
\pu{J g-1K-1}
Netočno
Točno
{{correctPercent}}%

Želite li pokušati ponovo?

Unesite odgovore na pripadajuća mjesta.

Dopunite rečenicu.

Standardne entalpije stvaranja (ΔfH°) nekih tvari pri 25 °C su:

ΔfH°(CaCO3(s)) = -1206,9 kJ/mol

ΔfH°(CaO(s)) = -635,5 kJ/mol

ΔfH°(CO2(g)) = -393,5 kJ/mol

\ce{CaCO3(s) -> CaO(s) + CO2(g)} \qquad \Delta_{\textrm{r}}H^\circ= \pu{177,9 \: kJ/mol}

Podsjetnik za računanje!

ΔrH° = H°P – H°R
ΔrH° = [∆fH°P – ∆fH°R]

Promjena je 

.

Pomoć!

Odaberi  i napiši točan odgovor:

a) egzotermna

b) endotermna

 

Netočno
Točno

Unesite odgovore na pripadajuća mjesta.

Dopunite rečenicu.

Izračunajte koliko se topline (Q) troši ili oslobađa za dobivanje 100,0 kg živog vapna.

Za dobivanje 100,0 kg živog vapna

se
kJ topline.

Netočno
Točno
{{correctPercent}}%

Želite li pokušati ponovo?

Unesite odgovore na pripadajuća mjesta.

Dopunite rečenicu.

Za reakciju žarenja vapnenca navedene su standardne entalpije stvaranja reaktanta i produkata pri 25 °C.

a) Izračunajte standardnu reakcijsku entalpiju i zaključite je li promjena egzotermna ili endotermna.

\ce{CaCO3(s) -> CaO(s) + CO2(g)} \qquad \Delta_{\textrm{r}}H^\circ = \pu{? \: kJ mol-1}

\Delta_{\textrm{f}}H^\circ(\ce{CaCO3},\textrm{s}) = \pu{-1206,9 \: kJ mol-1}
\Delta_{\textrm{f}}H^\circ(\ce{CaO},\textrm{s}) = \pu{-635,5 \: kJ mol-1}
\Delta_{\textrm{f}}H^\circ(\ce{CO2},\textrm{g}) = \pu{-393,5 \: kJ mol-1}

b) Izračunajte koliko se topline troši ili oslobađa za dobivanje 100,0 kg živog vapna.

Rješenje:

a) \Delta_{\textrm{r}}H^\circ =
kJ mol–1
Promjena je 
.

 

b) Za dobivanje 100,0 kg živog vapna
se
 × 105 kJ topline.
Netočno
Točno
{{correctPercent}}%

Želite li pokušati ponovo?

Riješeni primjer 1.

Izračunajte koliko je topline potrebno da se komad leda mase 55,5 g na temperaturi od –5,00 °C prevede u vodenu paru temperature 115 °C.

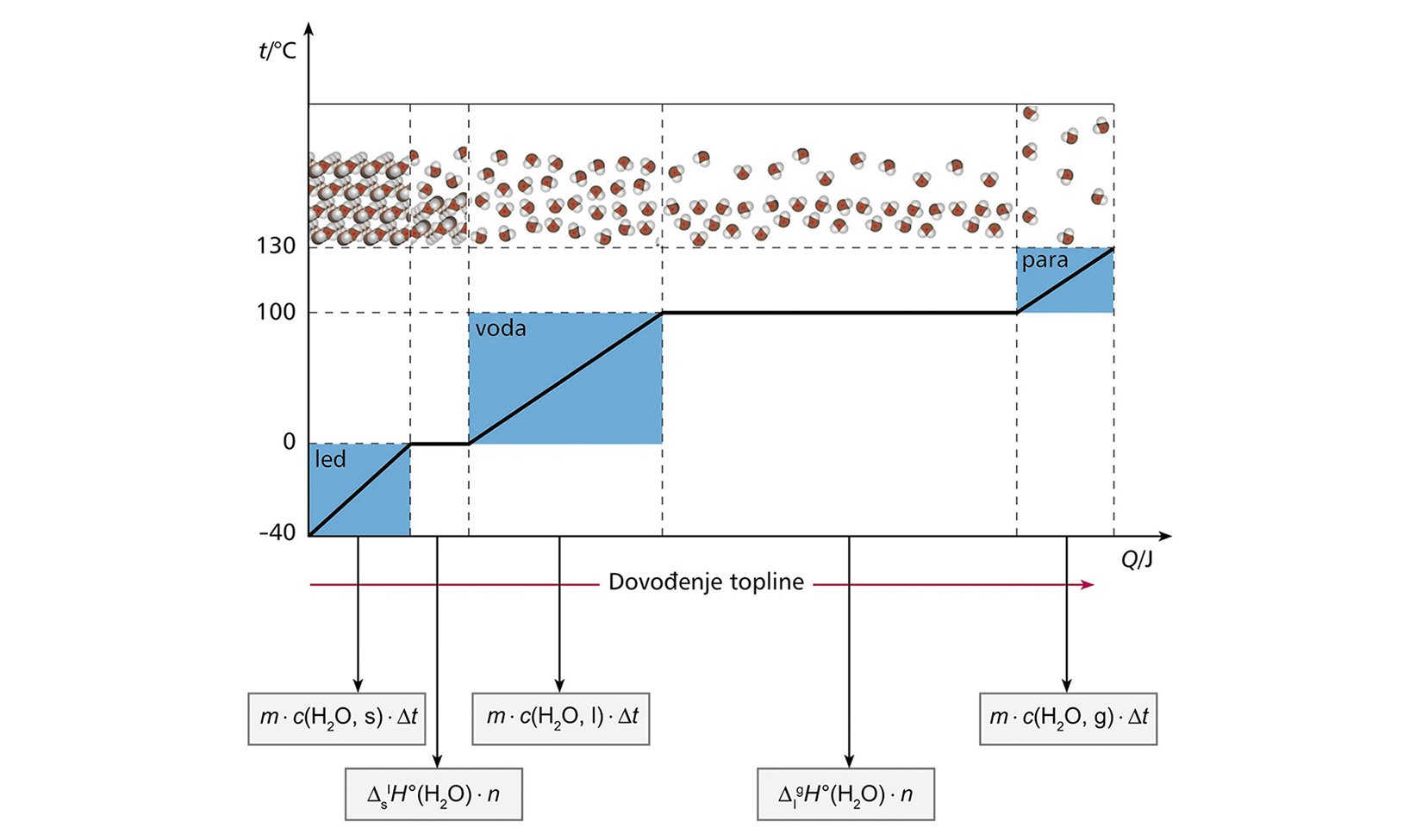
Zadano je:

m (led) = 55,5 g
t(led) = –5,00 °C
t(para) = 115 °C

c\textrm{(led)} =\pu{ 2,05 \: J\:g^{-1}K^{-1}}
c\textrm{(voda)} =\pu{ 4,18 \: J\:g^{-1}K^{-1}}
c\textrm{(para)} =\pu{ 2,03 \: J\:g^{-1}K^{-1}}

\Delta_{\textrm{s}}^{\textrm{l}}H^\circ=\pu{ 6,00\: kJ\: mol^{-1}}
\Delta_{\textrm{l}}^{\textrm{g}}H^\circ = \pu{40,7 \: kJ\: mol^{-1}}

\Delta_{\textrm{f}}H^\circ(\ce{C4H10},\textrm{g}) = \pu{-124,7 \: kJ mol-1}
\Delta_{\textrm{f}}H^\circ(\ce{CO2},\textrm{g}) = \pu{-393,5 \: kJ mol-1}
\Delta_{\textrm{f}}H^\circ(\ce{H2O},\textrm{g}) = \pu{-241,8 \: kJ mol-1}

Traži se:

Q = ?

Korak 1.

Q_{\textrm{ukupno}} = Q_1 + Q_2 + Q_3 + Q_4 + Q_5

Korak 2.
Q_1 = m(\textrm{led}) \cdot c(\textrm{led}) \cdot \Delta T
= \pu{55,5 g} \cdot \pu{2,05 J g-1 K-1} \cdot \pu{5,00 K}
= \pu{568,875 J}
= \pu{0,569 kJ}

Korak 3.

\begin{align} &Q_2 = \Delta_s^{l}H^\circ \cdot n(\textrm{led})\\ \\ & = \pu{6,00 \: kJ mol-1 \cdot} \: \dfrac{\pu{55,5 \: g}}{\pu{18,02 \: g\: mol^{-1}}}\\ \\ &\pu{ = 18,5 \:kJ }\\ \end{align}

Korak 4.

Q_3 = m(\ce{H2O}) \cdot c(\ce{H2O}) \cdot \Delta T
= \pu{55,5 g} \cdot \pu{4,18 J g-1 K-1}\cdot \pu{100 K}
= \pu{23199,0 J}
= \pu{23,2 kJ}

Korak 5.

\begin{align} &Q_4 = \Delta_{l}^{g}H^\circ \cdot n(\ce{H2O})\\ \\ &= \pu{40,7 \: kJ mol-1 \cdot} \: \dfrac{\pu{55,5 \: g}}{\pu{18,02 \:g mol-1}}\\ \\ & \pu{= 125 \:kJ }\\ \end{align}

Korak 6.

\begin{align} &Q_5 = m(\ce{H2O(g)}) \cdot c(\textrm{para}) \cdot\Delta T\\ \\ &\pu{ = 55,5 g \cdot \: 2,03 \: J g-1K-1 \cdot \: 15,0 K}\\ \\ &\pu{ = 1689,975 \:J }\\ \\ & \pu{= 1,69 \:kJ }\\ \end{align}

Korak 7.

Q_{\textrm{ukupno}} = Q_1 + Q_2 + Q_3 + Q_4 + Q_5
Q_{\textrm{ukupno}} = \pu{0,569 kJ} + \pu{18,5 kJ} + \pu{23,2 kJ} + \pu{125 kJ} + \pu{1,69 kJ}
\begin{align} &\Sigma Q = \pu{169,4 \:kJ} \\ & \Sigma Q = \pu{169 \:kJ }\\ \end{align}

(Rezultat je iskazan na tri značajne znamenke.)

Odgovor:
Da se komad leda mase 55,5 g pri temperaturi –5 °C prevede u vodenu paru na temperaturu 115 °C, potrebno je dovesti toplinu od 169 kJ.

Riješeni primjer 2.

Izračunajte masu butana koja će potpunim izgaranjem osloboditi toplinu od 169 kJ, toplinu potrebnu da se komad leda mase 55,5 g na temperaturi od –5,00 °C prevede u vodenu paru temperature 115 °C.

Zadano je:

m (led) = 55,5 g
t(led) = –5,00 °C
t(para) = 115 °C

\Delta_{\textrm{f}}H^\circ(\ce{C4H10},\textrm{g}) = \pu{-124,7 \: kJ mol-1}
\Delta_{\textrm{f}}H^\circ(\ce{CO2},\textrm{g}) = \pu{-393,5 \: kJ mol-1}
\Delta_{\textrm{f}}H^\circ(\ce{H2O},\textrm{g}) = \pu{-241,8 \: kJ mol-1}

Q = 169 kJ

Traži se:

m (C4H10) = ?

Korak 1.

\ce{C4H10(g) + \dfrac{13}{2}O2(g) -> 4CO2(g) + 5H2O(l)} \ce{2C4H10(g) + 13O2(g) -> 8CO2(g) + 10H2O(l)} \Delta_{\textrm{r}}H^\circ = [8 \cdot \Delta_{\textrm{f}}H^\circ(\ce{CO2(g)}) + 10 \cdot \Delta_{\textrm{f}}H^\circ(\ce{H2O(g)})] – [2 \cdot \Delta_{\textrm{f}}H^\circ(\ce{C4H10(g)})]

 

\pu{ = [8 \cdot ( -393,5 \: kJ mol-1) + 10 \cdot ( -241,8 kJ mol-1)] – [ 2 \cdot ( -124,7 \: kJ mol-1]} \pu{= [ -3148 \: kJ mol-1 + ( -2418 \: kJ mol-1)] – [ -249,4 \: kJ mol-1]} \pu{= -5566 \: kJ mol-1 + 249,4 \: kJ mol-1} \pu{= -5316,6 \: kJ mol-1}

 
Izgaranjem dva mola butana oslobodit će se toplina od \pu{5316,6 \: kJ mol-1} .

Korak 2.

m(\ce{C4H10}) = n(\ce{C4H10}) M(\ce{C4H10})
\pu{= 0,0636 \: mol \cdot 58,12 \: g mol-1}

\pu{= 3,70 \: g}

Odgovor:
Potpunim izgaranjem 3,70 g butana osobađa se toplina od 169 kJ koja je potrebna da se komad leda mase 55,5 g prevede u paru.

Unesite odgovore na pripadajuća mjesta.

Dopunite rečenicu.

Entalpijski dijagram nastajanja natrijevog klorida

Iz entalpijskog dijagrama nastajanja natrijevog klorida može se očitati da je:

Energija ionizacije natrija:
kJ mol-1
Elektronski afinitet klora:
kJ mol-1
Energija atomizacije klora:
kJ mol-1
Energija sublimacije natrija:
kJ mol-1
Entalpija stvaranja NaCl(s):
kJ mol-1
Energija kristalne rešetke NaCl(s):
kJ mol-1
Netočno
Točno
{{correctPercent}}%

Želite li pokušati ponovo?
Strukturna formula molekule benzena

Istraži - Što znamo o benzenu?

Što znamo o benzenu? Izvor slike: Generalić, Eni. "Benzen."

 

Više informacija o termodinamičkim procesima možete pronaći u modulu 2. Termodinamički sustavi i procesi u DOS-u Fizika 2.